Example Problem Post

Posted on January 2, 2009 by James Rohal | 1 Comment

This problem is from the Columbus State University problem of the week. Link

Problem

Given $a + 1 = b + 2 = c + 3 = d + 4 = a + b + c + d + 5$ , find the value of $a + b + c + d$ .

Solution

Note that this string of equalities gives us the following relations.

$a + 1 = b + 2$
$a + 1 = c + 3$
$a + 1= d + 4$
$a + 1 = a + b + c + d + 5$

We will first solve for $a$ which will in turn allow us to solve for the other values. Equations (1), (2), and (3) tell us that $b = a - 1$ , $c = a -2$ , and $d = a - 3$ , respectively. If we substitute these values into equation (4) we find

$a + 1 = a + (a- 1) + (a-2) + (a-3) + 5$

$2 = 3a$

$a = 2/3$

Thus we can use equations (1), (2), and (3) to find that $b = -1/3$ , $c = -4/3$ , and $d = -7/3$ . Their sum is

$a + b + c + d = 2/3 - 1/3 - 4/3 - 7/3 = -10/3$

This entry was posted in Problem and tagged columbus state university, latex. Bookmark the permalink.

One response to “Example Problem Post”

jamesrohal | January 2, 2009 at 10:53 pm |

Another way to solve this problem is using linear algebra. Note that the string of equalities gives us the following relations:
$-4 = b + c + d$
$-3 = a + c + d$
$-2 = a + b + d$
$-1 = a + b + c$
This allows us to set up two matrices:
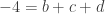
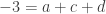
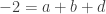
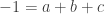
$A = \left[\begin{array}{cccc}0 & 1 & 1 & 1\\1 & 0 & 1 & 1\\1& 1& 0 & 1\\ 1& 1& 1& 0 \end{array}\right]$
and
$b = \left[\begin{array}{c}-4 \\ -3 \\ -2 \\ -1\end{array}\right]$
Then when you compute
$A^{-1}b = \left[\begin{array}{c}2/3 \\ -1/3 \\ -4/3 \\ -7/3\end{array}\right]$
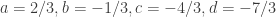you find $a = 2/3 , b = -1/3, c = -4/3, d = -7/3$ .